Well let me do my own bad paint work to illustrate my hypothesis. And to be clear, those charts are made up, not to scale, and I am not saying it works that way, I am asking whether it works that way.
So for a given drive, I assume there is a mix of better and weaker NAND cells, and I can create a histogram, where I sort them by DWPD (i.e. how many times each of those cells can be written), you would get a distribution like this (probably steeper, I have no idea), so stronger cells on the left, weaker cells on the right, adding up to a total of 4TB (native capacity of the drive):

So with no over provisionning, the disk sold as a 4TB retail drive would have a DWPD rating equal to its weakest cell, which in the illustration above would be 0.5 DWPD. It will have stronger cells but if the drive is full and, all cells have been written to 0.5 DWPD already, and you try to do one more write, the weakest cell will fail and the SSD will die.
Now with some factory over provisioning:
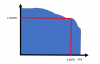
The disk only exposes 3.84TB of storage, so not only you distribute 3.84TB of writes on a slightly larger number of cells (4TB) but also if some of the weakest cells die, you can just retire them and you have enough stronger cells left to sustain 1DWPD. How much more DWPD depends on the distribution of the cells endurance.
And same logic if you do even more over provisioning:
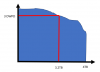
You can sustain a lot more DWPD because you allow a lot more of the weaker cells to die and still be able to do a full 3.2TB write.
So assuming it works the way above (and I don't even know if it is the case), what I was wondering is if by taking a 3.84TB drive and only partitioning 3.2TB, I am not giving the drive the same capacity to retire weaker cells once they start to fail than if the drive was factory limited to 3.2TB.



